Lab #8 (Part 1) - Introduction to PyTorch and Artificial Neural Networks

PyTorch is an open-source machine learning framework developed by AI researchers at Meta (Facebook). The torch library is not pre-installed in the Anaconda distribution, so you must add the torch and torchvision libraries yourself. You can do this by searching for them in the available libraries in your Anaconda environment.

If you've installed the torch library correctly, the following code should print a 3x2 tensor of zeros:

import torch
import torchvision
x = torch.zeros(3, 2)
print(x)

tensor([[0., 0.],
        [0., 0.],
        [0., 0.]])

Part 1 - Tensors

As alluded to in the introduction, the torch library uses its own type of data structure known as a tensor, which is similar to a multi-dimensional numpy array. The simplest tensors are just 1-dimensional arrays, or vectors.

Since the modeling of image data is one of the most successful applications of neural networks, we will begin this lab by learning how to represent images as tensors, as well as how to perform some basic manipulations on these tensors.

To begin, the code below reads the flattened form of 1000 examples from an image data set known as Fashion MNIST, which consists of 28x28 pixel grayscale images of 10 different types of fashion items:

### Read flattened, processed data
import pandas as pd
fash_mnist = pd.read_csv("https://remiller1450.github.io/data/fashion_mnist_train.csv")

## Train-test split
from sklearn.model_selection import train_test_split
train_fash, test_fash = train_test_split(fash_mnist, test_size=0.1, random_state=5)

### Separate the label column (outcome)
train_y = train_fash['y']
train_X = train_fash.drop(['y'], axis=1)
test_y = test_fash['y']
test_X = test_fash.drop(['y'], axis=1)

### Convert to numpy array then reshape to 900 by 28 by 28
mnist_unflattened = train_X.to_numpy()
mnist_unflattened = mnist_unflattened.reshape(900,28,28)

## Convert to tensor
mnist_tensor = torch.from_numpy(mnist_unflattened)

## Check shape of the first image
print(mnist_tensor[0,:,:].shape)

torch.Size([28, 28])

Notice that this code converted the training data, which was a pandas data frame, into a numpy array then reshaped it to have the dimensions 900, 28, 28. These dimensions correspond to the number of training examples, and the pixel layout of each example. An important benefit of storing these data as a tensor (rather than a flattened data frame) is that the spatial structure of the pixels within an example is preserved.

To provide additional context, one of these images (the 9th example) is displayed below. You can see how this exaxmple is stored in the tensor by printing the corresponding 28 x 28 tensor slice.

from skimage import io
io.imshow(mnist_unflattened[8,:,:])
# print(mnist_tensor[8,:,:]) ## Print if you'd like to see the tensor format

<matplotlib.image.AxesImage at 0x1833b303430>

In general, you can't expect to work with flattened grayscale images. Most modern machine learning methods involving image data are designed to work with tensors with dimensions: (N images, C color channels, w pixels, h pixels).

To better understand how to manipulate tensors into this format, we'll work with the following example image:

## Load an image and display it
my_img = io.imread("https://upload.wikimedia.org/wikipedia/commons/6/66/Polar_Bear_-_Alaska_%28cropped%29.jpg")
io.imshow(my_img)
io.show()

## Check the shape
my_img.shape

(565, 563, 3)

## Convert to tensor and check the shape
polar_bear = torch.from_numpy(my_img)
print(polar_bear.shape)

## Move third dimension (color channels) to the first dimension
polar_bear2 = torch.movedim(polar_bear, source=2, destination=0)
print(polar_bear2.shape)

## Add an empty first dimension, putting our tensor into the standard format
polar_bear_final = torch.unsqueeze(polar_bear2, dim=0)
print(polar_bear_final.shape)

torch.Size([565, 563, 3])
torch.Size([3, 565, 563])
torch.Size([1, 3, 565, 563])

Since the architecture of a neural network is characterized by the dimensions of the input tensor, we should have some familiarity with how to resize the pixel dimensions of an image's tensor:

from torch.nn import functional 
polar_bear_resized = functional.interpolate(polar_bear_final, size = (128,128))
print(polar_bear_resized.shape)

torch.Size([1, 3, 128, 128])

Resizing using interpolate will smooth over the higher resolution image to effectively reduce its size while preserving key details. We can view the resized image using the code below:

import matplotlib.pyplot as plt
polar_img_format = torch.movedim(polar_bear_resized[0], source=0, destination=2)
plt.imshow(polar_img_format)

<matplotlib.image.AxesImage at 0x157c6d4ca60>

You might note that imshow expects the image to have the form: (w pixels, h pixels, C color channels), so we needed to move the color channel dimension of our polar bear tensor.

Finally, you may want to save the resized image in a data folder for future use (as it's easiest to work with a folder of images with the same size):

from torchvision import transforms
from PIL import Image
transformed = transforms.ToPILImage()
transformed(polar_bear_resized[0]).save('polar_bear1.png')

You should note that are many different ways to save a processed image. The approach demonstrated above transforms the tensor to a PIL image prior to exporting it.

Additionally, you should note that we used interpolate to reduce the size of the polar bear image. However, best practice (assuming unlimited computational resources) would be to use interpolate to increase the size of the image to match the size of the largest images in the training database.

The examples in this lab will use the Fashion MNIST data, which won't require you to work with images of different sizes, or with images stored in a folder. However, you should be familar with these operations for your final project and this unit's homework assignment.

Question #1

The zipped folder at this link contains 50 images of cats.

• Part A - Download and unzip the folder (see above), then read the first example "cat.0" into Python and display it.
• Part B - Convert the image used in Part A to a tensor in conventional format. Print the dimensions of this tensor to verify your work.
• Part C - Resize pixel dimensions of the image from Parts A and B to 64x64 using the interpolate function.
• Part D - Display the resized image. Do you think this image retains sufficient information for a machine learning model to correctly classify it as a cat if it appeared in a database containing a mix of cats and dogs? Briefly explain. Hint: there's not necessarily a right or wrong answer, but you should think about whether the features a neural network might rely upon are preserved.

Part 2 - Network Architecture

To build a neural network model, we'll start by creating our own class named my_net that is a subclass of nn.Module. This class contains two important components:

1. A constructor that defines the pieces of the model's architecture using building blocks from nn.Module.
2. A forward function that organizes the network architecture by defining how an input tensor is forward propogated through the network.

The simple neural network created below is intended to work on the Fashion MNIST data. It's important to recognize that this dataset contains 28 x 28 pixel images with no color channel, so the network's expected input is an N by 28 by 28 tensor (hence the first layer begins with $28*28 = 784$ input features).

from torch import nn

class my_net(nn.Module):
    
    ## Constructor commands
    def __init__(self):
        super(my_net, self).__init__()
        
        ## Start by flattening each 28x28 image to 784 features
        self.flatten = nn.Flatten()
        
        ## Apply the following layers sequentially
        self.linear_relu_stack = nn.Sequential(
            nn.Linear(784, 512),
            nn.ReLU(),
            nn.Linear(512, 512),
            nn.ReLU(),
            nn.Linear(512, 10),
        )
    
    ## Function to generate predictions
    def forward(self, x):
        
        ## First it flattens x (note the capitalization, this is flatten() as defined above)
        x = self.flatten(x)
        
        ## Then it applies "linear_relu_stack()" (defined above)
        scores = self.linear_relu_stack(x)
        
        return scores

Question #2

• Part A - How many hidden layers does the network defined in the example above contain? How do you know this?
• Part B - What happens if the command self.flatten(x) is removed from the network's forward method? Briefly explain the issue.
• Part C - Briefly explain why we want the network's forward method to produce a 10-dimensional output.

Part 3 - Building Blocks

The operations performed within the stack of functions given in nn.Sequential might seem like a black box, so let's next explore how each of these components works using a few simple examples.

First, nn.Flatten will take any tensor and output a 2-dimensional tensor with dim 0 preserved from the original tensor. This will keep each observation separate, but collapse the rest of the tensor together.

## Create random tensor reflecting three 28 x 28 images
random_tensor = torch.rand(3,28,28)

## Flatten it and check the size
flatten = nn.Flatten()
flat_data = flatten(random_tensor)
print(flat_data.size())

torch.Size([3, 784])

Next, nn.Sequential is used to create an ordered sequence of layers that alternates between nn.Linear and nn.ReLU. Steps that use nn.Linear are applying linear transformations to their inputs and producing a specified number of outputs (neurons).

For example, we can visually understand the meaning of nn.Linear(3,2) using the diagram below:

## Sorry, this is an easy way to show images in HTML generated from a Python notebook
from IPython.display import HTML
HTML('<img src="https://www.sharetechnote.com/image/Python_Pytorch_nn_Linear_i3_o2_01.png">')

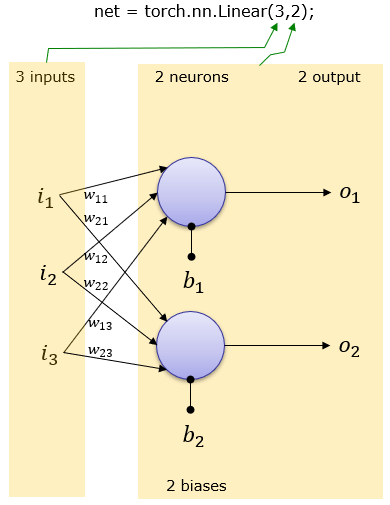
This layer maps 3 inputs into 2 outputs/neurons. For example, the first neuron, denoted $o_1$ in this diagram (which is what we've called $z^{(-)}$ in our lecture slides) is given by: $$o_1 = b_1 + w_{11}i_{1} + w_{12}i_{2} + w_{13}i_{3}$$

The numeric values of these weights and biases are learned from the data. In subsequent layers, the inputs $i_1, i_2, i_3$ may be features in the data or the outputs of earlier layers (following non-linear activation), or what we've denoted $a^{(-)}$ in our lecture slides.

We can further understand this structure by creating a simple network containing only this layer and printing its weights/biases (which are randomly initialized by default):

trial_net = torch.nn.Linear(3,2)
print(trial_net.weight)
print(trial_net.bias)

Parameter containing:
tensor([[-0.1938,  0.3906, -0.2316],
        [ 0.0665,  0.5100, -0.5428]], requires_grad=True)
Parameter containing:
tensor([ 0.2106, -0.0278], requires_grad=True)

Something else to note is that the weight and bias tensors contain an attribute requires_grad that is set to True. This setting means that quantities related to the gradient of these parameters will be calculated whenever the network is used. This is necessary if those weights/biases are to be updated as the network is trained. Later on we'll learn about transfer learning, in which we'll set this attribute to False in order to preserve certain weights in pre-trained networks.

Moving on, the steps that use nn.ReLU are introducing non-linearity via the rectified linear unit activation function). Recall that the ReLU function simply maps an input to itself if the input is positive and map it to zero otherwise.

Below is a demonstration of nn.ReLU:

## Create example hidden layer input
example_hidden_input = torch.FloatTensor([1.1, 2.2, -3.3, -0.1])

## Apply ReLU to input
nn.ReLU()(example_hidden_input)

tensor([1.1000, 2.2000, 0.0000, 0.0000])

You should note that activation does not introduce any new parameters into the model.

Question #3

• How many weights and biases are contained in the network my_net (defined previously)? Briefly explain, showing the details of any calculations you used.

Part 4 - Training the Network

To estimate the model's weights and biases using the training data, we need to begin by defining the following tuning parameters:

• Epochs - how many times the optimization algorithm should iterate over the training dataset
• Batch Size - how many observations should be used in each update iteration
• Learning Rate - how aggressively should the model's weights/biases change at each iteration

We also must specify an appropriate cost function and an optimzation algorithm (that is compatible with the chosen cost function).

## Hyperparms
epochs = 200
lrate = 0.01
bsize = 100

## Cost Function (cross entropy loss since the outcome is categorical)
cost_fn = nn.CrossEntropyLoss()

## Initialize the model
net = my_net()

## Optimizer (Stochastic Gradient Descent)
optimizer = torch.optim.SGD(net.parameters(), lr=lrate)

To help facilitate the passing of training examples into the network during learning, we'll use the DataLoader utilities that are part of PyTorch:

from torch.utils.data import DataLoader, TensorDataset
y_tensor = torch.Tensor(train_y)
train_loader = DataLoader(TensorDataset(mnist_tensor.type(torch.FloatTensor), y_tensor.type(torch.LongTensor)), batch_size=bsize)

This code creates a TensorDataset object that contains a tensor of predictors (which was stored in mnist_tensor) and a tensor of outcomes (y_tensor). Then, this TensorDataset object is used to create a DataLoader object that can be used to pass batches of data into the network.

The code provided below will train our network, which we named net, on the data contained train_loader by using the iterable nature of DataLoader objects to streamline the process:

import numpy as np

## Initial values for cost tracking
track_cost = np.zeros(epochs)
cur_cost = 0.0

## Loop through the data
for epoch in range(epochs):
    
    cur_cost = 0.0
    correct = 0.0
    
    ## train_loader is iterable and numbers knows the batch
    for i, data in enumerate(train_loader, 0):
        
        ## The input tensor and labels tensor for the current batch
        inputs, labels = data
        
        ## Clear the gradient from the previous batch
        optimizer.zero_grad()
        
        ## Provide the input tensor into the network to get outputs
        outputs = net(inputs)
        
        ## Calculate the cost for the current batch
        ## nn.Softmax is used because net outputs prediction scores and our cost function expects probabilities and labels
        cost = cost_fn(nn.Softmax(dim=1)(outputs), labels)
        
        ## Calculate the gradient
        cost.backward()
        
        ## Update the model parameters using the gradient
        optimizer.step()
        
        ## Track the current cost (accumulating across batches)
        cur_cost += cost.item()
    
    ## Store the accumulated cost at each epoch
    track_cost[epoch] = cur_cost
    # print(f"Epoch: {epoch} Cost: {cur_cost}") ## Uncomment this if you want printed updates

We can graph the cost by epoch to see if the weight estimates in our network have converged. Because we are using batches of data (stochastic gradient descent), we're looking for the cost to flatten out (with some noise).

import matplotlib.pyplot as plt
plt.plot(np.linspace(0, epochs, epochs), track_cost)
plt.show()

Here we can see that convergence has been reached.

Next, we'll calculate the classification accuracy for the training set:

## Initialize objects for counting correct/total 
correct = 0
total = 0

# Specify no changes to the gradient in the subsequent steps (since we're not using these data for training)
with torch.no_grad():
    for data in train_loader:
        # Current batch of data
        images, labels = data
        
        # pass each batch into the network
        outputs = net(images)
        
        # the class with the maximum score is what we choose as prediction
        _, predicted = torch.max(outputs.data, 1)
        
        # add size of the current batch
        total += labels.size(0)
        
        # add the number of correct predictions in the current batch
        correct += (predicted == labels).sum().item()

## Calculate and print the proportion correct
print(correct/total)

0.7911111111111111

The model's accuracy score on the training data is reasonable and shows that the model has learned (since we'd expect only 10% accuracy by chance); however, it might reflect the network overfitting to the training data, so we're more interested in the network's performance on the test data.

The code below reformats our test data into a TensorDataset, then puts into its own DataLoader object:

## Make test outcomes into a tensor
test_y_tensor = torch.Tensor(test_y.to_numpy())

### Convert to numpy array then reshape
test_unflattened = test_X.to_numpy().reshape(len(test_y),28,28)

## Convert test images into a tensor
test_tensor = torch.from_numpy(test_unflattened)

## Combine X and y tensors into a TensorDataset and DataLoader
test_loader = DataLoader(TensorDataset(test_tensor.type(torch.FloatTensor), test_y_tensor.type(torch.LongTensor)), batch_size=bsize)

We can now use test_loader in the same evaluation loop we previously used:

## Repeat evaluation loop suing the test data
correct = 0
total = 0
with torch.no_grad():
    for data in test_loader:
        images, labels = data
        outputs = net(images)
        _, predicted = torch.max(outputs.data, 1)
        total += labels.size(0)
        correct += (predicted == labels).sum().item()
print(correct/total)

0.75

Comments: In theory you could use cross-validation to obtain an unbiased estimate of your network's performance on new data. You could use this to help you to decide when to stop training, or whether a tweak in the model's architecture is beneficial. However, training a neural network is already computationally demanding (even for a relatively small dataset like Fashion MNIST), so we will not demonstrate the approach here as $k$-fold cross validation will increase the computational time by roughly a factor of $k$. If you are interested, this article provides an example of how to use the KFold function in sklearn and SubsetRandomSampler in pytorch to perform k-fold cross validation.

Part 5 - Application

The zipped folder at this link contains 50 images of cats and 100 images of dogs (chihuahua breed).

I have resized these images for you, so you won't need to worry about their dimensions. I've included my code for this procedure (for the cats images) if you are curious (perhaps for the purposes of your final project). This code was adapted from this StackOverflow answer and it is not necessary that you run it on your own PC (I also did not share the dogs folder).

path = 'OneDrive - Grinnell College/Documents/cats/'
for item in os.listdir(path):
        if os.path.isfile(path+item):
            im = Image.open(path+item)
            f, e = os.path.splitext(path+item)
            imResize = im.resize((64,64), Image.Resampling.LANCZOS)
            imResize.save(path + 'new/' + item, 'JPEG')

The code provided below will load all of these images into a numpy array:

import os
import matplotlib.pyplot as plt
path = 'OneDrive - Grinnell College/Documents/cats_dogs/'
img_names = os.listdir(path)

images = np.empty(shape = (150, 64, 64, 3))
for idx, name in enumerate(img_names):
    img_name = path + name
    # Use you favourite library to load the image
    image = plt.imread(img_name)
    images[idx] = image

Note that these images are ordered, so we'll set up the target labels manually. If this were not the case we could extract the labels from the image file names.

## We'll use 1 = cat, 0 = dog
classes = [1,0] 

## Repeat an appropriate number of times (print to check)
labels = np.repeat(classes, [50, 100], axis=0)
labels

array([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0])

To confirm that the data have loaded properly, you can try displaying a single example:

import matplotlib.pyplot as plt
plt.imshow(images[10].astype('uint8'))

<matplotlib.image.AxesImage at 0x157ce70d460>

Note that we had to cast the pixel intensities to integers so that they are properly handled by imshow.

Question #4

• Part A - Perform a 75-25 training-testing split on the data described above that is stored in the objects images and labels. See the second example in the documentation if you've never used this function when the outcome/target variable has already been separated from the predictors.
• Part B - Create a neural network model containing 3 hidden layers. You may choose the number of neurons contained in each layer, but you should be careful to specify a valid architecture. Your network should begin by flattening the input tensor before it is supplied to the hidden layers. Each layer, with the exception of the final output layer, should be followed by ReLU activation function.
• Part C - Convert the training and testing data from Part A into properly formated tensors that are stored as DataLoader objects.
• Part D - Train your network for 10 epochs, applying softmax to the network output and using the cross entropy cost function. You should try to manipulate the learning rate and network architecture to get the network to learn something from the training (ie: get the cost to improve), but you shouldn't be disappointed if you cannot get it to do so (since this is a miniscule amount of data for this type of application). If your code properly updates the network's weights and tracks the cost you will receive credit for this question.
• Part E - Evaluate your network on the test data and print the classifcation accuracy.

Image credits:

1. https://www.sharetechnote.com/html/Python_PyTorch_nn_Linear_01