from IPython.display import HTML
HTML('<img src="https://learnopencv.com/wp-content/uploads/2019/05/transfer-learning-1024x574.jpg">')
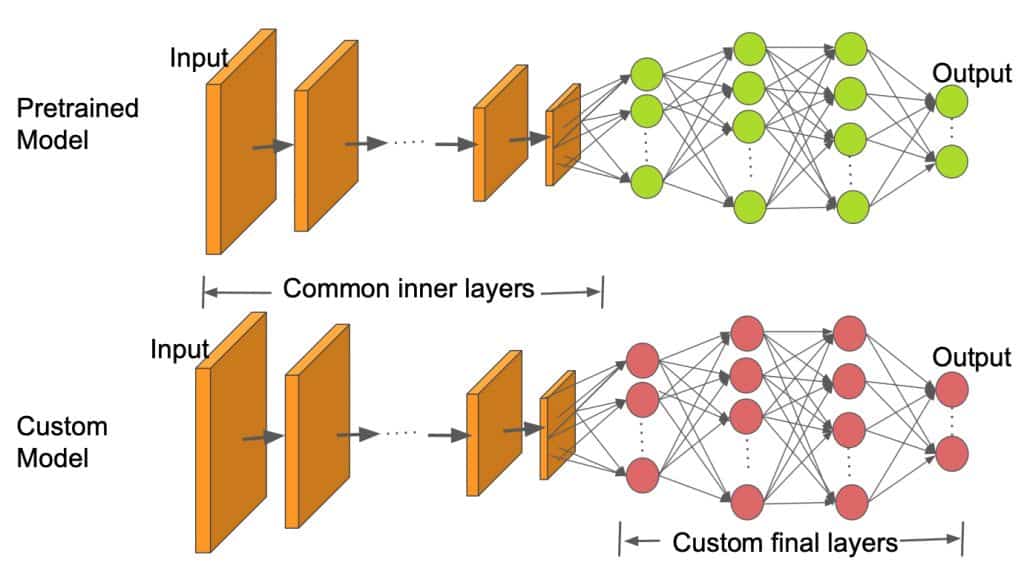
This lab introduces transfer learning as a strategy for adapting pre-trained neural networks to specific applications.
The lab will use functions in the torch libraries:
import torch
import torchvision
import numpy as np
The examples during the lab will use the Fashion MNIST dataset, and we'll see if we can achieve better classification performance than our previous models by adapting pretrained neural networks.
Convolutional neural networks are a powerful deep learning framework, but it's rare to have sufficient data to effectively train a complex network entirely from scratch.
These issues have given rise to the popularity of transfer learning, which is a general term used to describe the adaptation or reuse of a previously trained model on a new task. For example, we'll later adapt a model that performed well on the ImageNet data to classify the 150 dogs and cats we've seen in our previous labs. The basic idea behind this would be that this model has already learned many features that could be useful in distinguishing cats from dogs.
There are two common approaches to transfer learning. The first is to use the pretrained model as a "feature extractor" by removing one or more of its later layers and replacing them with new layers that will be trained using the new data. The parameters in earlier layers of the model are "frozen", meaning they aren't updated via back-propogation as the model trains on the new data. Thus, the newly added layers end up learning how to use the features that are identified by the existing layers to make accurate predictions.
The diagram below provides a visual illustration of this framework:
from IPython.display import HTML
HTML('<img src="https://learnopencv.com/wp-content/uploads/2019/05/transfer-learning-1024x574.jpg">')

The second approach is to "fine-tune" a pretrained network.
This approach again requires replacing one or more of the final layers with ones of your own; however, you'll also allow the weights and biases in the earlier layers of the model that were retained to be updated during back-propogation while training the network on your new data.
You might view this approach as using the weights from the pretrained network as an excellent choice of initial values (rather than randomly initializing weights as our previous "from scratch" models had done). When adopting a "fine-tuning" approach, you should be particularly careful with the learning rate you use. It's generally most effective to set a small learning rate, as it's quite easy to overfit your data when using this strategy.
The torch library includes a variety of pretrained models across several different machine learning domains:
For our examples, we'll use the "EfficientNet" model introduced in this paper. For context, EfficientNet is a convolutional neural network that uses unique scaling approaches to achieve imporved computational efficiency and achieve greater generalizability. There are actually several versions of EfficientNet, and the top EfficientNet models have proven themselves to be very effective in transfer learning, achieving near state-of-the-art performance levels on benchmark computer vision datasets like CIFAR-100.
To make this lab as computationally efficient as possible, we'll use the "b0" version of this model, which is the smallest of the EfficientNet models. That said, this model still contains roughly 5.3 million parameters, so the notion of "small" is relative.
The code below obtains the estimated weights that EfficientNet b0 learned from the ImageNet database, and it sets up a model with the EfficientNet b0 architecture using those weights:
efnet_weights = torchvision.models.EfficientNet_B0_Weights.DEFAULT
efnet_model = torchvision.models.efficientnet_b0(weights = efnet_weights)
If you print efnet_model (by uncommenting the code below), you'll see that the model is very deep and contains many convolutional layers. If you examine the final layer, you'll notice that EfficientNet generates an outcome vector of length 1000.
# print(efnet_model) # Uncomment if curious, the output is very long
Because the architecture of any neural network is designed for the characteristics of the data that it was trained on, we should be aware of input data that was used by EfficientNet.
In general, the pretrained models in torch handle data transformations automatically as preprocessing steps. We can print these transformations to better understand the format of the data used to train the model:
print(efnet_weights.transforms())
ImageClassification(
crop_size=[224]
resize_size=[256]
mean=[0.485, 0.456, 0.406]
std=[0.229, 0.224, 0.225]
interpolation=InterpolationMode.BICUBIC
)
We can see that the EfficientNet normalizes the three color channels using means of ~0.45 and standard deviations of ~0.22, it resizes the images to 256 by 256 pixels using BICUBIC interpolation, then it performs a central crop to produce a 224 by 224 pixel image.
We don't actually need to worry about most of these steps, as they will be applied automatically to input data that is passed into the EfficientNet model. However, we do need to worry about the fact that EfficientNet expects input images with 3 color channels. Because the Fashion MNIST images have a single color channel, we'll need to duplicate this channel 3 times to obtain suitable input tensors.
### Read flattened, processed data
import pandas as pd
fash_mnist = pd.read_csv("https://remiller1450.github.io/data/fashion_mnist_train.csv")
## Train-test split
from sklearn.model_selection import train_test_split
train_fash, test_fash = train_test_split(fash_mnist, test_size=0.1, random_state=5)
### Separate the label column (outcome)
train_y = train_fash['y']
train_X = train_fash.drop(['y'], axis=1)
test_y = test_fash['y']
test_X = test_fash.drop(['y'], axis=1)
### Convert to numpy array then reshape to 900 by 28 by 28
mnist_unflattened = train_X.to_numpy()
mnist_unflattened = mnist_unflattened.reshape(900,28,28)
## Convert to tensor
mnist_tensor = torch.from_numpy(mnist_unflattened)
mnist_tensor = torch.unsqueeze(mnist_tensor, dim=1)
## Transform to proper input shape (duplicate the single color channel to produce 3 channels)
new_mnist_tensors = mnist_tensor.expand(-1, 3, -1, -1)
## Store in DataLoader
from torch.utils.data import DataLoader, TensorDataset
y_tensor = torch.Tensor(train_y)
train_loader = DataLoader(TensorDataset(new_mnist_tensors.type(torch.FloatTensor), y_tensor.type(torch.LongTensor)), batch_size=100)
Dropout(...). After briefly reading the documentation on this operation, explain in your own words what this function is doing and how it might benefit the performance of the network.Two basic operations we must consider for transfer learning using a pretrained model are:
If you had previously printed the architecture of EfficientNet, you may have noticed that the model contains three different named components that each contain one or more of the building blocks used in torch. The first and largest of these model components is named "features", while the others are named "avgpool" and "classifier".
In our first example of transfer learning we will adopt the "feature extraction" approach on the Fashion MNIST data. To achieve this, we will "freeze" everything in the "features" portion of the network by changing the requires_grad attribute of those parameters to False:
## Loop through each parameter and set `requires_grad` to false
for param in efnet_model.features.parameters():
param.requires_grad = False
Next, we need to modify the final layer of the network so that its outputs are appropriate for our application. Since fashion MNIST contains 10 classes, we'll want 10 outputs from the model's final layer. We will also remove the dropout layer, but you could keep it if you wanted to.
## Replace the "classifier" layer with one for our application
efnet_model.classifier = torch.nn.Sequential(
torch.nn.Linear(in_features=1280, out_features=10, bias=True))
Perhaps surprisingly, these simple commands are all that are necessary to prepare our transfer learning model that uses EfficientNet.
requires_grad to False for this piece of the model? Briefly explain.The training loop below will use the Fashion MNIST data to learn the parameters that are trainable in our model. Because this network is far more complex than the models we built from scratch, training may take a long time. Even though back-propogation is only done for the trainable layers, the each training example must be forward-propogated through the entire network.
## Hyperparms
epochs = 100
lrate = 0.1
## Cost Function
from torch import nn
cost_fn = nn.CrossEntropyLoss()
## Network model
torch.manual_seed(7) # For reproduction purposes (should be minor since only the last layers are randomly intialized)
net = efnet_model
## Optimizer (using ADAM, a more flexible algorithm than SGD this time)
optimizer = torch.optim.Adam(net.parameters(), lr=lrate)
## Initial values for cost tracking
track_cost = np.zeros(epochs)
cur_cost = 0.0
## Loop through the data
for epoch in range(epochs):
cur_cost = 0.0
correct = 0.0
## train_loader is iterable and numbers knows the batch
for i, data in enumerate(train_loader, 0):
## The input tensor and labels tensor for the current batch
inputs, labels = data
## Clear the gradient from the previous batch
optimizer.zero_grad()
## Provide the input tensor into the network to get outputs
outputs = net(inputs)
## Calculate the cost for the current batch
## nn.Softmax is used because net outputs prediction scores and our cost function expects probabilities and labels
cost = cost_fn(nn.Softmax(dim=1)(outputs), labels)
## Calculate the gradient
cost.backward()
## Update the model parameters using the gradient
optimizer.step()
## Track the current cost (accumulating across batches)
cur_cost += cost.item()
## Store the accumulated cost at each epoch
track_cost[epoch] = cur_cost
# print(f"Epoch: {epoch} Cost: {cur_cost}") ## Uncomment this if you want printed updates
import matplotlib.pyplot as plt
plt.plot(np.linspace(0, epochs, epochs), track_cost)
plt.show()
From the graph shown above, we can see that the cost seems to still be improving; however, we'll stop here since training this network takes so much longer than the networks we've trained in our previous labs.
Furthermore, as seen below, this network already achieves reasonable level of classification accuracy on the Fashion MNIST data. Better performance can likely be achieved with more training, and we might not be overly concerned with overfitting yet since most of the network's parameters are "frozen".
## Initialize objects for counting correct/total
correct = 0
total = 0
# Specify no changes to the gradient in the subsequent steps (since we're not using these data for training)
with torch.no_grad():
for data in train_loader:
# Current batch of data
images, labels = data
# pass each batch into the network
outputs = net(images)
# the class with the maximum score is what we choose as prediction
_, predicted = torch.max(outputs.data, 1)
# add size of the current batch
total += labels.size(0)
# add the number of correct predictions in the current batch
correct += (predicted == labels).sum().item()
## Calculate and print the proportion correct
print(correct/total)
0.7522222222222222
If we wanted to adopt the "fine-tuning" approach to transfer learning, all we need to do is reintialize our model from EfficientNet and modify the model's final layers. Alternatively, we could keep our existing transfer learning model and "unfreeze" the parameters that were previously frozen. This second approach comes with the added benefit of the final layer starting the next round of training with a better set of initial parameters (since we'd previously trained them).
## "unfreeze" parameters
for param in net.features.parameters():
param.requires_grad = True
When training this model, we'll want to be more careful to choose a small learning rate, since it's much easier to overfit our training data now that all 5.3 million parameters can be updated. Let's now train the entire model for 100 additional epochs and see what happens.
## ## Hyperparms
epochs = 100
lrate = 0.00001
## Cost Function
cost_fn = nn.CrossEntropyLoss()
## Optimizer (using a more flexible algorithm than SGD this time)
optimizer = torch.optim.Adam(net.parameters(), lr=lrate)
## Initial values for cost tracking
import numpy as np
track_cost = np.zeros(epochs)
cur_cost = 0.0
## Loop through the data
for epoch in range(epochs):
cur_cost = 0.0
correct = 0.0
## train_loader is iterable and numbers knows the batch
for i, data in enumerate(train_loader, 0):
## The input tensor and labels tensor for the current batch
inputs, labels = data
## Clear the gradient from the previous batch
optimizer.zero_grad()
## Provide the input tensor into the network to get outputs
outputs = net(inputs)
## Calculate the cost for the current batch
## nn.Softmax is used because net outputs prediction scores and our cost function expects probabilities and labels
cost = cost_fn(nn.Softmax(dim=1)(outputs), labels)
## Calculate the gradient
cost.backward()
## Update the model parameters using the gradient
optimizer.step()
## Track the current cost (accumulating across batches)
cur_cost += cost.item()
## Store the accumulated cost at each epoch
track_cost[epoch] = cur_cost
# print(f"Epoch: {epoch} Cost: {cur_cost}") ## Uncomment this if you want printed updates
As you probably noticed, training all of the networks parameters is substantially more computationally intensive, so let's hope that this approach pays off with an improved classification accuracy:
## Initialize objects for counting correct/total
correct = 0
total = 0
# Specify no changes to the gradient in the subsequent steps (since we're not using these data for training)
with torch.no_grad():
for data in train_loader:
# Current batch of data
images, labels = data
# pass each batch into the network
outputs = net(images)
# the class with the maximum score is what we choose as prediction
_, predicted = torch.max(outputs.data, 1)
# add size of the current batch
total += labels.size(0)
# add the number of correct predictions in the current batch
correct += (predicted == labels).sum().item()
## Calculate and print the proportion correct
print(correct/total)
0.8277777777777777
This model seems to perform better than any model we've built up until this point, or at least it does so on the training data.
Let's now use the test data to get an unbiased assessment of its performance:
## Make test outcomes into a tensor
test_y_tensor = torch.Tensor(test_y.to_numpy())
### Convert to numpy array then reshape
test_unflattened = test_X.to_numpy().reshape(len(test_y),1,28,28)
## Convert test images into a tensor
test_tensor = torch.from_numpy(test_unflattened)
## Expand to have 3 channels
test_tensor = test_tensor.expand(-1, 3, -1, -1)
## Combine X and y tensors into a TensorDataset and DataLoader
test_loader = DataLoader(TensorDataset(test_tensor.type(torch.FloatTensor),
test_y_tensor.type(torch.LongTensor)), batch_size=100)
## Repeat evaluation loop suing the test data
correct = 0
total = 0
with torch.no_grad():
for data in test_loader:
images, labels = data
outputs = net(images)
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
print(correct/total)
0.49
Unfortunately, this overfit the training data. A common strategy this scenario is to introduce a validation set, which is kept separate from the training data and is used to calculate the model's error (cost) at each training epoch, but is not used to update/train the model.
If you were exclusively interested in a single model (as you might be here), it's reasonable to use what we had previously designated to be the test set as our validation set. In general, you might want separate validation and test sets if you wanted a truly unbiased estimate of your model's performance on new data.
The code below provides a quick demonstration (though it's only quick if you don't run the given code):
## Reload the EfficientNet model
efnet_weights = torchvision.models.EfficientNet_B0_Weights.DEFAULT
efnet_model = torchvision.models.efficientnet_b0(weights = efnet_weights)
## Freeze parameters
for param in efnet_model.features.parameters():
param.requires_grad = False
## Set up new classifier layer
efnet_model.classifier = torch.nn.Sequential(torch.nn.Linear(in_features=1280, out_features=10, bias=True))
## Initialize with same random seed as before
torch.manual_seed(7)
net = efnet_model
## ## Hyperparms
epochs = 100
lrate = 0.1
## Cost Function
from torch import nn
cost_fn = nn.CrossEntropyLoss()
## Optimizer (using a more flexible algorithm than SGD this time)
optimizer = torch.optim.Adam(net.parameters(), lr=lrate)
## Initial values for cost tracking
track_cost = np.zeros(epochs)
track_val_cost = np.zeros(epochs)
cur_cost = 0.0
val_cur_cost = 0.0
## Loop through the data
for epoch in range(epochs):
cur_cost = 0.0
val_cur_cost = 0.0
## train_loader is iterable and numbers knows the batch
for i, data in enumerate(train_loader, 0):
## The input tensor and labels tensor for the current batch
inputs, labels = data
## Clear the gradient from the previous batch
optimizer.zero_grad()
## Provide the input tensor into the network to get outputs
outputs = net(inputs)
## Calculate the cost for the current batch
## nn.Softmax is used because net outputs prediction scores and our cost function expects probabilities and labels
cost = cost_fn(nn.Softmax(dim=1)(outputs), labels)
## Calculate the gradient
cost.backward()
## Update the model parameters using the gradient
optimizer.step()
cur_cost += cost.item()
for i, data in enumerate(test_loader, 0):
inputs, labels = data
val_outputs = net(inputs)
val_cost = cost_fn(nn.Softmax(dim=1)(val_outputs), labels)
val_cur_cost += val_cost.item()
## Store the accumulated cost at each epoch
track_cost[epoch] = cur_cost
track_val_cost[epoch] = 9*val_cur_cost ## Multiplying by 9 puts these on the same scale
# print(f"Epoch: {epoch} Cost: {cur_cost} Validation Cost: {val_cur_cost}") ## Uncomment this if you want printed updates
import matplotlib.pyplot as plt
plt.plot(np.linspace(0, epochs, epochs), np.column_stack((track_cost, track_val_cost)))
plt.show()
Here we can see that while the cost continues to decrease on the training data, it doesn't seem to improve much for the validation data. We could use a graph like this one to help us determine when to stop training our network.
For this question you will again revisit the cats vs. dogs data contained in the zipped folder at this link. I promise that this is the last time I'll ask you to classify the cats and dogs in this folder.
Previously, we saw that we weren't able to learn anything useful with a vanilla artificial neural network, but a convolutional neural network and data augmentation allowed us to achieve classification performance that was better than random guessing. We'll now see if transfer learning can help us do even better.
random_state=5. Then, store a properly formatted version of the training data in a DataLoader object that uses a batch size of 28.