from IPython.display import HTML
HTML('<img src="https://learnopencv.com/wp-content/uploads/2019/05/transfer-learning-1024x574.jpg">')
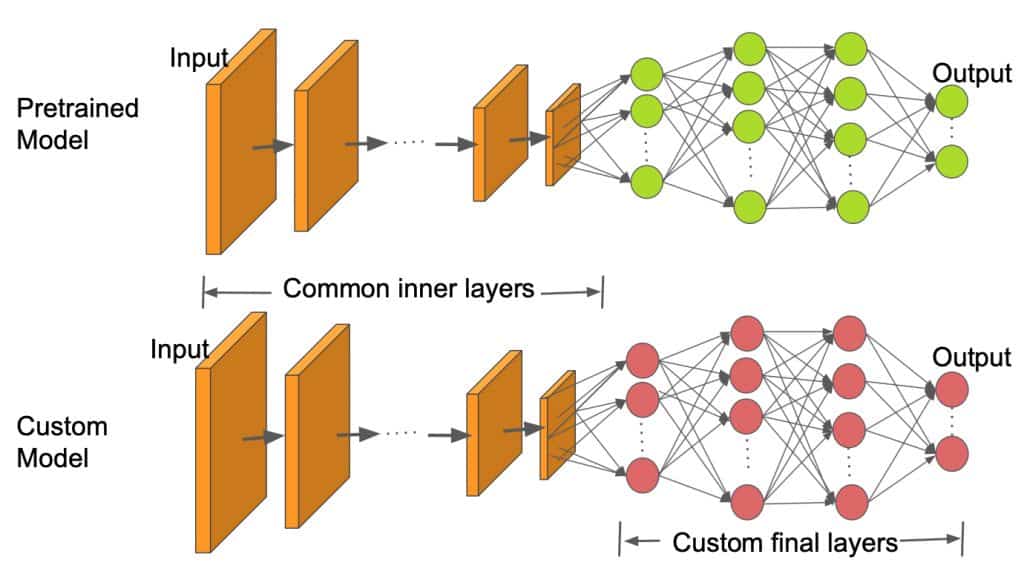
This lab covers the topic of transfer learning, or taking a pre-trained deep learning model and adapting it for a specific task.
## Torch libraries
import torch
import torchvision
import numpy as np
Our examples will continue to use the Fashion MNIST data set, and there will be questions the cats vs. dogs images you worked with in our previous two labs. The goal will be to investigate how we can improve upon our past performances by exploiting the features learned by pre-trained models.
Convolutional neural networks have proven to be extremely successful at working with image and video data. However, a massive amount of training data and computational resources are required to train an effective network from scratch. For context:
For these reasons, many applications of machine learning using transfer learning approaches, a general term that describes the adaptation or reuse of a previously trained model on a new task. For example, we'll adapt a model that performed well on the ImageNet data to classify the 150 dogs and cats from our previous labs. The basic idea behind here is that the pre-trained model has already learned how to identify a number of low-level features that can be useful for distinguishing between cats and dogs.
Transfer Learning Approach #1 - Feature Extraction:
There are two common approaches to transfer learning. The first is to use the pretrained model as a "feature extractor" by removing one or more of its later layers and replacing them with new layers that will be trained using the new data. The parameters in earlier layers of the model are "frozen", meaning they aren't updated via back-propogation as the model trains on the new data. Thus, the newly added layers end up learning how to use the features that are identified by the existing layers to make accurate predictions.
The diagram below provides a visual illustration of this framework:
from IPython.display import HTML
HTML('<img src="https://learnopencv.com/wp-content/uploads/2019/05/transfer-learning-1024x574.jpg">')

Transfer Learning Approach #2 - Fine Tuning:
This approach also requires replacing one or more of the final layers with ones of your own; however, this time you'll allow the weights and biases in the earlier layers of the model to be updated during back-propogation while training the network on your new data (rather than being frozen in place as was done in the feature extraction approach).
You could view the approach of using the weights from a pretrained network as an excellent choice of initial values (rather than randomly initializing weights as our previous "from scratch" models had done). However, when adopting a "fine-tuning" approach, you should be especially careful with the learning rate you choose. It's generally most effective to set a small learning rate, as it's easy to overfit if the early layers of the network are allowed to substantially change to adapt to small details found in your training data.
The torch library includes a variety of pretrained models across several different machine learning domains:
-This documentation page provides additional information on the available models and their intended applications.
For our examples, we'll use the "EfficientNet" model introduced in this paper. For context, EfficientNet is a convolutional neural network that uses unique scaling approaches in order to achieve better computational efficiency and greater generalizability. There are several versions of EfficientNet, and the top EfficientNet models have proven themselves to be very effective in transfer learning, achieving near state-of-the-art performance levels on benchmark computer vision datasets like CIFAR-100.
To the run times in this lab as efficient as possible, we'll use the "b0" version of this model, which is the smallest of the EfficientNet models. That said, this model still contains roughly 5.3 million parameters, so the notion of it being "small" is relative.
The code below obtains the estimated weights that EfficientNet b0 learned from training on the ImageNet database. It then sets up a model with the EfficientNet b0 architecture using those weights:
## Load efficient net b0 weights
efnet_weights = torchvision.models.EfficientNet_B0_Weights.DEFAULT
## Set up efficientnet_b0 model using those weights
efnet_model = torchvision.models.efficientnet_b0(weights = efnet_weights)
If you're curious, you can print efnet_model (by uncommenting the code below). From this you'll see that the model's architecture is deep and contains several convolutional layers. Important to notice is that the final layer outputs a vector of length 1000.
# print(efnet_model) # Uncomment if curious, the output is very long
Because the architecture of any neural network is designed for the characteristics of the data that it was trained on, we should be aware of the structure of the input data used to train EfficientNet.
Fortunately, it's usually the case that the pretrained models in torch are set up to handle data transformations automatically as preprocessing steps. We can print these transformations to better understand the format of the data used to train the model:
## Efficient net preprocessing transforms
print(efnet_weights.transforms())
ImageClassification(
crop_size=[224]
resize_size=[256]
mean=[0.485, 0.456, 0.406]
std=[0.229, 0.224, 0.225]
interpolation=InterpolationMode.BICUBIC
)
We can see that the EfficientNet normalizes each image's three color channels using means of ~0.45 and standard deviations of ~0.22, it resizes the image to 256 by 256 pixels using BICUBIC interpolation, before applying a central crop to produce a 224 by 224 pixel image.
We don't actually need to worry about most of these steps, as they will be applied automatically to input data that is passed into the EfficientNet model. The one exception is that, we do need to worry about the fact that EfficientNet expects input images with 3 color channels. Since the Fashion MNIST images only have a single color channel, we'll need to duplicate this channel 3 times to make our input data suitable for the EfficientNet architecture.
### Read flattened, processed data
import pandas as pd
fash_mnist = pd.read_csv("https://remiller1450.github.io/data/fashion_mnist_train.csv")
## Train-test split
from sklearn.model_selection import train_test_split
train_fash, test_fash = train_test_split(fash_mnist, test_size=0.1, random_state=5)
### Separate the label column (outcome)
train_y = train_fash['y']
train_X = train_fash.drop(['y'], axis=1)
test_y = test_fash['y']
test_X = test_fash.drop(['y'], axis=1)
### Convert to numpy array then reshape to 900 by 28 by 28
mnist_unflattened = train_X.to_numpy()
mnist_unflattened = mnist_unflattened.reshape(900,28,28)
## Convert to tensor
mnist_tensor = torch.from_numpy(mnist_unflattened)
mnist_tensor = torch.unsqueeze(mnist_tensor, dim=1)
## Transform to proper input shape (duplicate the single color channel to produce 3 channels)
new_mnist_tensors = mnist_tensor.expand(-1, 3, -1, -1)
## Store in DataLoader
from torch.utils.data import DataLoader, TensorDataset
y_tensor = torch.Tensor(train_y)
train_loader = DataLoader(TensorDataset(new_mnist_tensors.type(torch.FloatTensor), y_tensor.type(torch.LongTensor)), batch_size=100)
Question #1:
There are two basic operations we must consider for transfer learning using a pretrained model are:
If you had previously printed the architecture of EfficientNet, you may have noticed that the model contains three different named components that each contain one or more of the building blocks used in torch. The first and largest of these model components is named "features", while the others are named "avgpool" and "classifier".
In this portion of the lab we'll try a "feature extraction" approach on the Fashion MNIST data. This will require us to "freeze" everything in the "features" portion of the network by changing the requires_grad attribute of those parameters to False:
## Loop through each parameter and set `requires_grad` to false
for param in efnet_model.features.parameters():
param.requires_grad = False
Next, we need to modify the final layer of the network so that its outputs are appropriate for our application. More specifically, because the fashion MNIST contains 10 classes, we'll want 10 outputs in the model's final layer. The code given below also removes the dropout layer, but you could keep it if you wanted to.
## Replace the existing "classifier" layer with our own creation
efnet_model.classifier = torch.nn.Sequential(
torch.nn.Linear(in_features=1280, out_features=10, bias=True))
Perhaps surprisingly, this is all that's necessary to implement the feature extraction approach and we're ready to try out our model.
Question #2
requires_grad to False for this portion of the model? Briefly explain.The training loop below uses the Fashion MNIST data to learn the parameters that are trainable in our model. Because this network is far more complex than the models we built from scratch, training can take a long time. Even though backpropogation is only done for the trainable layers, the each training example must be forward propogated through the entire network.
## Hyperparms
epochs = 100
lrate = 0.1
## Cost Function
from torch import nn
cost_fn = nn.CrossEntropyLoss()
## Network model
torch.manual_seed(7) # For reproduction purposes (should be minor since only the last layers are randomly intialized)
net = efnet_model
## Optimizer (using ADAM, a more flexible algorithm than SGD this time)
optimizer = torch.optim.Adam(net.parameters(), lr=lrate)
## Initial values for cost tracking
track_cost = np.zeros(epochs)
cur_cost = 0.0
## Loop through the data
for epoch in range(epochs):
cur_cost = 0.0
correct = 0.0
## train_loader is iterable and numbers knows the batch
for i, data in enumerate(train_loader, 0):
## The input tensor and labels tensor for the current batch
inputs, labels = data
## Clear the gradient from the previous batch
optimizer.zero_grad()
## Provide the input tensor into the network to get outputs
outputs = net(inputs)
## Calculate the cost for the current batch
## nn.Softmax is used because net outputs prediction scores and our cost function expects probabilities and labels
cost = cost_fn(nn.Softmax(dim=1)(outputs), labels)
## Calculate the gradient
cost.backward()
## Update the model parameters using the gradient
optimizer.step()
## Track the current cost (accumulating across batches)
cur_cost += cost.item()
## Store the accumulated cost at each epoch
track_cost[epoch] = cur_cost
# print(f"Epoch: {epoch} Cost: {cur_cost}")
## Print the cost curve
import matplotlib.pyplot as plt
plt.plot(np.linspace(0, epochs, epochs), track_cost)
plt.show()
Looking at the graph shown above, the cost seems to still be improving; but, we'll stop here since training this network takes so much longer than the networks we've trained in our previous labs.
Furthermore, as seen below, this network already achieves reasonable level of classification accuracy on the Fashion MNIST data. But its reasonable to believe that better performance can be achieved with more training, and we might not be overly concerned with overfitting since most of the network's parameters are "frozen".
## Initialize objects for counting correct/total
correct = 0
total = 0
# Specify no changes to the gradient in the subsequent steps (since we're not using these data for training)
with torch.no_grad():
for data in train_loader:
# Current batch of data
images, labels = data
# pass each batch into the network
outputs = net(images)
# the class with the maximum score is what we choose as prediction
_, predicted = torch.max(outputs.data, 1)
# add size of the current batch
total += labels.size(0)
# add the number of correct predictions in the current batch
correct += (predicted == labels).sum().item()
## Calculate and print the proportion correct
print(correct/total)
0.7255555555555555
If we wanted to adopt the "fine-tuning" approach to transfer learning, all we would need to do is reintialize our model and modify the model's final layers. That is, we'd repeat the same initial steps shown in this lab without modifying the requires_grad attribute.
Alternatively, we could start with our feature extraction transfer learning model and "unfreeze" the parameters that were previously frozen. This approach is preferrable because the model's final layers have effective initial values rather than randomly generated weights.
## Start w/ our prior model and "unfreeze" parameters
for param in net.features.parameters():
param.requires_grad = True
As was mentioned earlier in the lab, we'll want to be more careful to choose a small learning rate here, since it's much easier to overfit our training data now that all 5.3 million parameters can be updated.
Let's now train the entire model for 100 additional epochs and see how it does on the Fashion MNIST data:
## ## Hyperparms
epochs = 100
lrate = 0.00001
## Cost Function
cost_fn = nn.CrossEntropyLoss()
## Optimizer (using a more flexible algorithm than SGD this time)
optimizer = torch.optim.Adam(net.parameters(), lr=lrate)
## Initial values for cost tracking
import numpy as np
track_cost = np.zeros(epochs)
cur_cost = 0.0
## Loop through the data
for epoch in range(epochs):
cur_cost = 0.0
correct = 0.0
## train_loader is iterable and numbers knows the batch
for i, data in enumerate(train_loader, 0):
## The input tensor and labels tensor for the current batch
inputs, labels = data
## Clear the gradient from the previous batch
optimizer.zero_grad()
## Provide the input tensor into the network to get outputs
outputs = net(inputs)
## Calculate the cost for the current batch
## nn.Softmax is used because net outputs prediction scores and our cost function expects probabilities and labels
cost = cost_fn(nn.Softmax(dim=1)(outputs), labels)
## Calculate the gradient
cost.backward()
## Update the model parameters using the gradient
optimizer.step()
## Track the current cost (accumulating across batches)
cur_cost += cost.item()
## Store the accumulated cost at each epoch
track_cost[epoch] = cur_cost
# print(f"Epoch: {epoch} Cost: {cur_cost}") ## Uncomment this if you want printed updates
As you've surely noticed, training all of the network's 5.3 million parameters is substantially more computationally intensive than "feature extraction", so let's hope that this approach paid off with an improved classification accuracy:
## Initialize objects for counting correct/total
correct = 0
total = 0
# Specify no changes to the gradient in the subsequent steps (since we're not using these data for training)
with torch.no_grad():
for data in train_loader:
# Current batch of data
images, labels = data
# pass each batch into the network
outputs = net(images)
# the class with the maximum score is what we choose as prediction
_, predicted = torch.max(outputs.data, 1)
# add size of the current batch
total += labels.size(0)
# add the number of correct predictions in the current batch
correct += (predicted == labels).sum().item()
## Calculate and print the proportion correct
print(correct/total)
0.7988888888888889
This model seems to perform better than any model we've built up until this point, or at least it does so on the training data.
Let's now use the test data to get an unbiased assessment of its performance:
## Make test outcomes into a tensor
test_y_tensor = torch.Tensor(test_y.to_numpy())
## Convert to numpy array then reshape
test_unflattened = test_X.to_numpy().reshape(len(test_y),1,28,28)
## Convert test images into a tensor
test_tensor = torch.from_numpy(test_unflattened)
## Expand to have 3 channels
test_tensor = test_tensor.expand(-1, 3, -1, -1)
## Combine X and y tensors into a TensorDataset and DataLoader
test_loader = DataLoader(TensorDataset(test_tensor.type(torch.FloatTensor),
test_y_tensor.type(torch.LongTensor)), batch_size=100)
## Repeat evaluation loop suing the test data
correct = 0
total = 0
with torch.no_grad():
for data in test_loader:
images, labels = data
outputs = net(images)
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
print(correct/total)
0.51
Unfortunately, our model overfit the training data. This is a common problem in transfer learning, and a popular strategy is to use a single validation set and keep track of the cost (error) on that set during each training epoch. If the cost on the validation set starts to increase by a significant amount the training process is halted.
If you were exclusively interested in a single model (as you might be here), it's reasonable to use what we had previously designated to be the test set as our validation set. In general, you might want separate validation and test sets if you wanted a truly unbiased estimate of your model's performance on new data.
The code below provides a demonstration of this approach:
## Reload the EfficientNet model
efnet_weights = torchvision.models.EfficientNet_B0_Weights.DEFAULT
efnet_model = torchvision.models.efficientnet_b0(weights = efnet_weights)
## Freeze parameters
for param in efnet_model.features.parameters():
param.requires_grad = False
## Set up new classifier layer
efnet_model.classifier = torch.nn.Sequential(torch.nn.Linear(in_features=1280, out_features=10, bias=True))
## Initialize with same random seed as before
torch.manual_seed(7)
net = efnet_model
## ## Hyperparms
epochs = 100
lrate = 0.1
## Cost Function
from torch import nn
cost_fn = nn.CrossEntropyLoss()
## Optimizer (using a more flexible algorithm than SGD this time)
optimizer = torch.optim.Adam(net.parameters(), lr=lrate)
## Initial values for cost tracking
track_cost = np.zeros(epochs)
track_val_cost = np.zeros(epochs)
cur_cost = 0.0
val_cur_cost = 0.0
## Loop through the data
for epoch in range(epochs):
cur_cost = 0.0
val_cur_cost = 0.0
## train_loader is iterable and numbers knows the batch
for i, data in enumerate(train_loader, 0):
## The input tensor and labels tensor for the current batch
inputs, labels = data
## Clear the gradient from the previous batch
optimizer.zero_grad()
## Provide the input tensor into the network to get outputs
outputs = net(inputs)
## Calculate the cost for the current batch
## nn.Softmax is used because net outputs prediction scores and our cost function expects probabilities and labels
cost = cost_fn(nn.Softmax(dim=1)(outputs), labels)
## Calculate the gradient
cost.backward()
## Update the model parameters using the gradient
optimizer.step()
cur_cost += cost.item()
for i, data in enumerate(test_loader, 0):
inputs, labels = data
val_outputs = net(inputs)
val_cost = cost_fn(nn.Softmax(dim=1)(val_outputs), labels)
val_cur_cost += val_cost.item()
## Store the accumulated cost at each epoch
track_cost[epoch] = cur_cost
track_val_cost[epoch] = 9*val_cur_cost ## Multiplying by 9 puts these on the same scale
# print(f"Epoch: {epoch} Cost: {cur_cost} Validation Cost: {val_cur_cost}") ## Uncomment this if you want printed updates
## Plot cost curves for both training and validation sets
plt.plot(np.linspace(0, epochs, epochs), np.column_stack((track_cost, track_val_cost)))
plt.show()
Here we can see that while the cost continues to decrease on the training data, it doesn't seem to improve much for the validation data.
Question 3: For this question you will again revisit the cats vs. dogs data contained in the zipped folder at this link. I promise you this is the last time I'll ask you to classify these cats and dogs.
Previously, we saw that we weren't able to learn anything useful with a vanilla artificial neural network, but a convolutional neural network and data augmentation allowed us to achieve classification performance that was better than random guessing. We'll now see if transfer learning can help us do even better.
random_state=5. Then, store a properly formatted version of the training data in a DataLoader object that uses a batch size of 28.